TrigonoMetri

TrigonoMetri adalah suatu peghitungan dalam sistem Matematika yang digunakan dalam menghitung sudut. Aturan ini berlaku pada segitiga siku-siku. Aturan TrigonoMetri ini didasari oleh prinsip Phytagoras yang menyatakan bahwa kuadrat dari sisi miring sebuah segitiga siku-siku sama dengan jumlah dari kuadrat kedua sisi lainnya.


Berikut adalah pengitungannya.

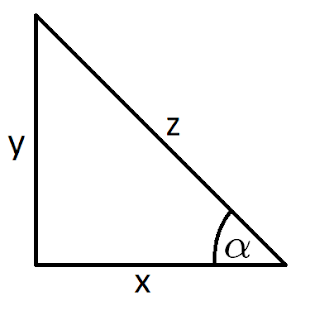Segitiga siku-siku dengan sisi x,y, dan z dengan sudut α

Jika dipantau dari segitiga di atas, terdapat 2 sisi yang saling ttegak lurus dan 1 sisi miring pada segitiga tersebut. Sesuai dengan aturan Phytagoras, maka X² + Y²= Z²
Dari aturan tersebut maka dapat ditentukan melalui penghitungan yang rumit dan didapatkan teori dasar trigonometri yang berupa:

$ sin \alpha =\frac{y}{z} $
$ cos \alpha =\frac{x}{z} $
$ tan \alpha = \frac{sin \alpha}{cos \alpha} = \frac{y}{x} $
dengan α sebagai sudut yang sudah ditandai seperti diatas dan nilai α sudah diketahui.

Dari ketiga bentuk dasar diatas, terdapat pula inversnya, yaitu mencari sudut dari sisi - sisi segitiga yang panjangnya diketahui, dikenal dengan sebutan arc-, yang notasinya adalah bentuk pangkat -1 pada bentuk TrigonoMetri-nya, sebagai berikut:

$ sin^{-1} (\frac{y}{z}) = \arcsin(\frac{y}{z}) = \alpha $
$ cos^{-1} (\frac{x}{z}) = \arccos(\frac{x}{z}) = \alpha $
$ tan^{-1} (\frac{y}{x}) = \arctan(\frac{y}{x}) = \alpha $

Namun demikian, dengan bentuk pangkat -1 tersebut berarti bentuk seper- , untuk bentuk 1/sinα, 1/cosα, dan 1/tanα memiliki sebutan yang berbeda lagi dari yang sebelumnya, yaitu cosecan, secan, dan cotangen, dengan detailnya sebagai berikut:

$ \frac{1}{sin \alpha} = cosec  \alpha = csc  \alpha $
$ \frac{1}{cos \alpha} = sec  \alpha$
$ \frac{1}{tan \alpha} = cot  \alpha$

Sekian mengenai materi TrigonoMetri Dasar ini. Bila ada tanggapan/saran silakan ditulis di kolom komentar di bawah. Untuk yang lebih lanjut mengenai sifat TrigonoMetri dapat dibaca disini. Terima Kasih telah membaca.